Oscillations - Online Test

Answer : Option D
Explaination / Solution:

If the restoring force of a vibrating or oscillatory system is proportional to the displacement
of the body from its equilibrium position and is directed opposite to the direction of displacement,
the motion of the system is simple harmonic and it is given by
x(t)=Acosωt
where A, the maximum value of the displacement, is called the amplitude of the motion. If
T is the time for one complete oscillation, then
x(t + T) = x(t)

Acosω(t+T)=Acosωt
ωT=2π
or T=2πω
 As angular frequency ω  is given by ω=km−−√ and T=2πω

 Then,time period of oscillation of mass m is given by

T=2πmk−−√

Answer : Option C
Explaination / Solution:
No Explaination.

Answer : Option B
Explaination / Solution:

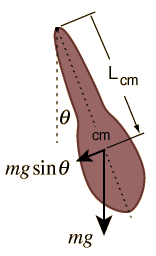
Torque;τ=Iα,a= angular accleration

τ=−mglsinθ∴α≃mglθI

α=−ω2θω=mglI−−−√

so Time period T is :

T = 2π
  Imgl−−−√

Answer : Option B
Explaination / Solution:

The energy is dissipitaed as it decreases in the exponential form , making the amplitude to zero ultimately . every pendulam in non ideal condition behaves like damped system, where damping force which is proportional to velocity is offered it by air resistance the fig shows the damped motion where the amplittude of the succesive oscillayion is damped by an exponential fuction of time

Answer : Option B
Explaination / Solution:

Damping is proportional to the velocity of the mass through the medium , so it can be said that air drag ,friction offers damping.

Answer : Option C
Explaination / Solution:

In real oscillators, friction, or damping, slows the motion of the system. Due to frictional force, the velocity decreases in proportion to the acting frictional force. 

F=−cdxdt

where the c is the damping constant

Answer : Option B
Explaination / Solution:

The forces on the system is restoring force F=−kx   and the damping force is F=−bv=−bdxdt    where  'k' is the force constant and 'b' is the damping constant

The net force is F= m*a  which is equal to the sum of restoring force F=−kx   and the damping force is F=−bv=−bdxdt

md2xdt2=−kx−bdxdt∴md2xdt2+kx+bdxdt=0

Answer : Option A
Explaination / Solution:

The damped natural frequency fd is related to the natural frequency fn by a  relation 

 fd=fn1−ζ2−−−−−√

where damping ratio ζ  is <= 1 

so the fd is less than the natural frequency 

Answer : Option A
Explaination / Solution:

The free damping oscillations contains the forces as acceleration forces, damping and spring forces, But in the case of forced oscillations there is an external force that acts to maintain the vibrations that usually gets damped due to presence of the damping forces like friction, air drag etc. the presence of the force promote to the Total Mechanical Energy relations.

Answer : Option C
Explaination / Solution:

When the mass and spring have no external force acting on them they transfer energy back and forth at a rate equal to the natural frequency. In other words, to efficiently pump energy into both mass and spring requires that the energy source feed the energy in at a rate equal to the natural frequency. Applying a force to the mass and spring is similar to pushing a child on swing, a push is needed at the correct moment to make the swing get higher and higher. As in the case of the swing, the force applied need not be high to get large motions, but must just add energy to the system. The damper, instead of storing energy, dissipates energy. Since the damping force is proportional to the velocity, the more the motion, the more the damper dissipates the energy. Therefore, there is a point when the energy dissipated by the damper equals the energy added by the force. At this point, the system has reached its maximum amplitude and will continue to vibrate at this level as long as the force applied stays the same. If no damping exists, there is nothing to dissipate the energy and, theoretically, the motion will continue to grow into infinity.