Integrals - Online Test
Q1. The function is
Answer : Option B
Explaination / Solution:
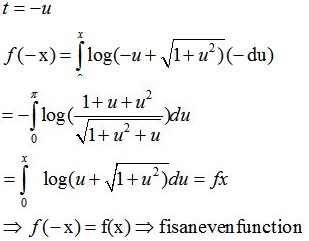
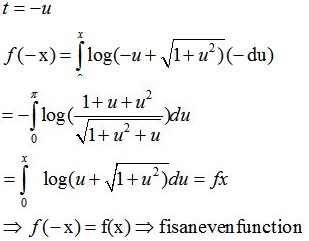
Q2. t dt is equal to
Answer : Option C
Explaination / Solution:
=[sint]π/2−π/2=sinπ2−sin(−π2)=1+1=2
Q3. dx is equal to
Answer : Option D
Explaination / Solution:


Q4. is equal to
Answer : Option A
Explaination / Solution:


Q5. is equal to
Answer : Option B
Explaination / Solution:


Q6. dx is equal to
Answer : Option D
Explaination / Solution:


Q7. is equal to
Answer : Option A
Explaination / Solution:
Note that is an odd function, therefore,
Q8. (tan x) dx is equal to
Answer : Option D
Explaination / Solution:


Q9. (cot x) dx is equal to
Answer : Option A
Explaination / Solution:


Q10. is equal to
Answer : Option A
Explaination / Solution: